File information
Created by
AsteriskAmpersand and MoonbunnieUploaded by
AsteriskAmpersandVirus scan
About this mod
Redefines the gunner defense penalty curving so that it handles extreme values better.
- Requirements
- Permissions and credits
SUMMARY:
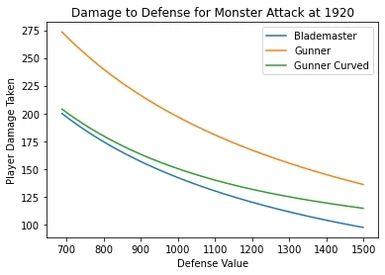
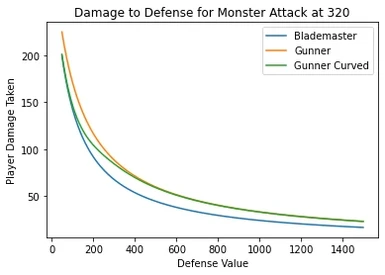
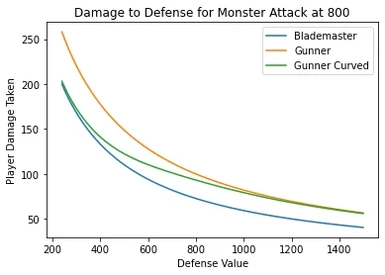
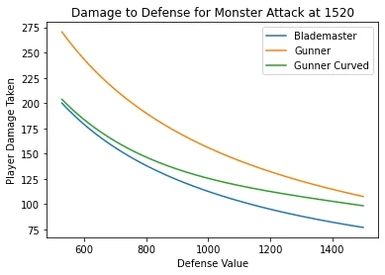
Changes the gunner defense penalty to scale inversely proportional to monster raw atttack values. Mitigating the extreme difference at the extremes of the damage spectrum from the fixed modifier. Gunners are taken out of one shot range on a fair number of attacks while still taking increased damage and still being within one shot range when blademasters are.
QUICK DETAILS:
The gunner defense penalty was first introduced in base game. The way it operates and how the curve is related to the blademaster damage curve for similar values made sense for values within the parameters defined there. With Iceborne there was no revision of the system but values got more extreme. Finally with the Fatalis updates, there's a considerable departure between values involved in the formula, to the point it's not functioning within it's intended range. A problem of scaling difficulty just by inflating numbers in both attack and defense but not paying attention to the structure of the underlying formula.
This mod aims to correct this by applying a curve modifier to the gunner defense penalty so it's dependent on monster attack values and scales accordingly to avoid the extreme value distortions that occur on post-game content.
This mod upholds 5 major principles:
- Higher player armor values should result in less damage taken from the same attack
- Higher monster attack values should result in more damage taken form the same attack
- Gunners should take more damage than Blademasters
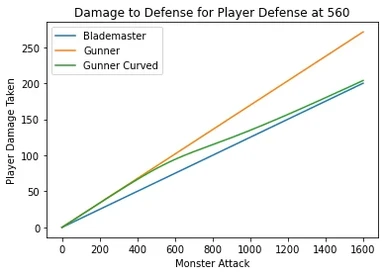
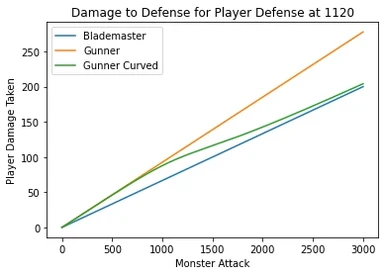
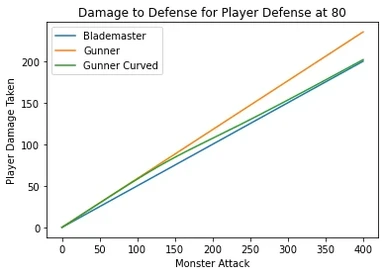
- Below 80 points of damage the penalty should behave similarly to base game
- Above 190 damage gunners should be taking damage closer to blademasters.
Acknowledgements:
Thanks to Moonbunnie for his work in researching the damage function entry points, the defense formula and related mechanics, helping debug issues with mathematical improprieties within the code and just generally being a great friend/co-modmaker.
Support the Mod Maker:
Patreon support is highly appreciated: https://www.patreon.com/user?u=21034864
Direct donations as well: https://www.paypal.me/AsteriskAmpersand?locale.x=en_US
LONG EXPLANATION:
The damage formula:
The damage formula absent item and skill buffs is a function in 3 variables, Monster Raw, Player Defense and the Player Class
Let D: RxRx(0.7,1) -> R
D(MonsterRaw, PlayerDefense, Class) = MonsterRaw* 80/(PlayerDefense*Class+80)
We shall label the damage taken by blademasters D_BM, and the damage taken by gunners D_G:
D_BM(x,y) = D(x,y,1)
D_G(x,y) = D(x,y,0.7)
Let D_G0 be the modified gunner damage function
D_G0 : RxR -> R
D_G0 (x,y)
The principles formalized:
We formally define the above major principles in strict terms
D_G0 must satisfy:
- d D_G0 /dx >= 0
- d D_G0 /dy < 0
- D_BM(x,y) <= D_G0(x,y) <= D_G(x,y)
- For every (x,y) in D_BM^(-1)(190)
D_G0(x,y) - 190 <=5 - For every (x,y) in D_G^(-1)(80)
The first two are the "sanity" conditions. More armor should always result in less damage. More Monster Raw should always result in more damage.
3rd is the balance condition, Gunner damage should be more or equal to blademaster and less or equal to original gunner
Fourth and Fifth are the "mix-in points" conditions
To satisfy this conditions the implementation is done through a smoothing coefficient produced through a base sigmoid.
The smoothing sigmoid:
Using a smoothing coefficient function S(k,y) where for every k0 S(k0,y) is a member of a sigmoid family and S(x,y) is smooth on xsuch that S(k,y) = 0, S(k,inf) = 1
dS/dx > 0
dS/dy > 0
any sigmoid-like fulfils this properties as long as we add 1 to them and then halve them (sigmoids are restricted to -1,1 in their image)
D_G0 = H
D_G = G
D_BM = F
H(x,y) = G(x,y)*(1-S(x,y)) + F(x,y)*(S(x,y))
dH/dx = dG/dx*(1-S(x,y)) + dF/dx*(S(x,y)) + F(x,y)*dS/dx - G(x,y)*dS/dx
dH/dy = dG/dy*(1-S(x,y)) + dF/dy*(S(x,y)) + F(x,y)*dS/dy - G(x,y)*dS/dy
dG/dx,dF/dx,S(x,y) and 1-S(x,y) are always positive functions and dF/dy, dG/dy are always negative so in reality our only worry is that
dG/dx*(1-S(x,y)) + dF/dx*(S(x,y)) + F(x,y)*dS/dx > G(x,y)*dS/dx
dG/dy*(1-S(x,y)) + dF/dy*(S(x,y)) + F(x,y)*dS/dy < G(x,y)*dS/dy
we know from the structure that blademaster damage will always surpass gunner, so F(x,y) > G(x,y) furthermore dS/dx and dS/dy are positive as long as we are careful on the sigmoid composition, thus F(x,y)*dS/dx > G(x,y)*dS/dx and F(x,y)*dS/dy > G(x,y)*dS/dy
F(x,y) <= H(x,y) <= G(x,y) follows from the fact that the sigmoid is bound to [-1,1] and we are performing a convex sum of functions
The explicit sigmoid:
The chosen smoothing sigmoid is:
s(x) = (x/sqrt(1+x^2))
After applying the necessary domain transformation and biasing it to it's more extreme ends:
S(x) = ((s(x) +1)/2 )^2
We must now transform the input domain so that the sigmoid shape matches the desired transformation boundaries.
For this purpose we define:
SmoothingFactor = 4
RightEnd = (PlayerDefense+80)*160/80
LeftEnd = (PlayerDefense*.7+80)*-20/80
Center = (RightEnd +LeftEnd )/2
Span = (RightEnd - LeftEnd )
The values for the right and left end were experimentally chosen after multiple empirical trials of the function within in-game conditions.
Thus the final smoothing coefficient function is defined as:
a(MonsterAttack,PlayerDefense) = ((S(((MonsterAttack - center)*SmoothingFactor/Span)+1)/2)^2
The explicit new damage function:
We can then define:
H(MonsterAttack,PlayerDefense) = F(MonsterAttack,PlayerDefense)*(a(MonsterAttack,PlayerDefense)) +
G(MonsterAttack,PlayerDefense)*(1-a(MonsterAttack,PlayerDefense))
Which the astute reader will be able to tell is a convex sum over the blademaster and gunner damage formulas over a unit bound parameter.
A big caveat:
A limitation of this method is that this does not take into account the usage of skills and items, and directly outputs a damage instead of modifying the defense of the player before the rest of calculations.
To solve this issue we simply must solve the damage equation for the Player Defense value which would yield equivalent damage.
Given our new damage formula
H(x,y) = x * ( (80/(y+80))*(1-a(x,y)) + (80/(y*.7+80))*a(x,y))
We can also have the equivalent damage formula
H0(x,y) = x * 80/(z(x,y)+80)
Where z is the new player defense value such that H(x,y) = H0(x,y)
Expanding the equality we have:
x * 80/(z(x,y)+80) = x * ( (80/(y+80))*(1-a(x,y)) + (80/(y*.7+80))*a(x,y))
We then solve the equation for z which yields:
z = y * (240 * a(x,y) + 7 * y + 560 ) / ( (10 - 3 * a(x,y)) * y + 800)
And thus we have a new player defense value which has been curved and fulfils all of the properties defined above.
But what about elemental gunner bonus?:
The gunner defense penalty also applies to elemental resistance and for most of the curve it will just overpower it. The bonus is already extremely small and any sort of fraction will always shrink it beyond blademaster values. Even when the values match with blademaster, because of how elemental resist works, it's insignificant. Monster attacks mostly consist of raw damage, even the most extreme case barely scrape a 30% of the damage from an attack. Furthermore the scaling of elemental resistance is basically non-existant, player armor values are simply too small to make any considerable reduction in it. To get a visible damage reduction you need something on the triple digit regions while player values hover on the low teens and the gunner bonus barely accounts for a single point or more, normally it's a negative value because the gunner penalty is still active anyway.
If you've reached this far, congratulations, you've far exceeded my faith in the average nexus user, feel free to contact me on discord and tell me you got through the swamp that is first year calculus and endless pontificating.